参考相关:“关于pcm音频头与a-law音频头的互换代码” http://blog.csdn.net/fjhyy/article/details/6593049
https://baike.baidu.com/item/A%E5%BE%8B/5923040
http://www.sohu.com/a/147745747_464086
背景:正在做的一个项目,需要网络传输音频,音频格式为wav,16位采样率,PCM编码。为了降低传输带宽,需要对音频数据进行压缩。
把16bit的音频数据转为8bit。
最简单的方式是均匀量化, >>8 (右移8位),但这样做会使得声音的噪音变大。
最好的做法是使用非均匀量化(如A-Law),其原理是对于小音量的声音,其蕴含的信息量更大,人耳对小音量
更敏感;而大音量部分则影响没那么大。因此使用非均匀量化的方式,对于小音量部分保留更多的数据,大音量部分
则保留更少的数据。具体实现如下:
这里选择A-Law(A律)算法,也可以用uLaw(μ律),两种算法可相互转化。
令量化器过载电压为1,相当于把输入信号进行归一化,那么A律对数压缩定义为:
当0 <= x <= 1/A时,f(x)=(Ax)/(1+lnA)
当1/A <= x <= 1时,f(x)=(1+lnAx)/(1+lnA)
在现行的国际标准中A=87.6,此时信号很小时(即小信号时),从上式可以看到信号被放大了16倍,
这相当于A压缩率与无压缩特性比较,对于小信号的情况,量化间隔比均匀量化时减小了16倍,
因此,量化误差大大降低;而对于大信号的情况例如x=1,量化间隔比均匀量化时增大了5.47倍,
量化误差增大了。这样实际上就实现了“压大补小”的效果。
图形曲线如下(只画出正数部分,对于负数也是同样的道理)(这里用了归一化):
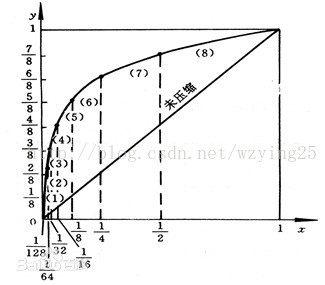
但是要在程序中实现该曲线,比较复杂。因此这里使用8段折线来近似表示。
把x轴划分为不均匀的8份,第一点取1/2处,第二点取1/4处,第三点取1/8处……第七点取1/128.
把y轴划分为均匀的8分段。
代码实现如下:
A-Law算法实现PCM压缩.c
#include "stdio.h"
#define SIGN_BIT (0x80) /* Sign bit for a A-law byte. */
#define QUANT_MASK (0xf) /* Quantization field mask. */
#define NSEGS (8) /* Number of A-law segments. */
#define SEG_SHIFT (4) /* Left shift for segment number. */
#define SEG_MASK (0x70) /* Segment field mask. */
static short seg_end[8] = {0xFF, 0x1FF, 0x3FF, 0x7FF,
0xFFF, 0x1FFF, 0x3FFF, 0x7FFF}; //分成不均匀的8个分段,算上负数,总共是16个分段
/* copy from CCITT G.711 specifications */
unsigned char _u2a[128] = { /* u- to A-law conversions */
1, 1, 2, 2, 3, 3, 4, 4,
5, 5, 6, 6, 7, 7, 8, 8,
9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24,
25, 27, 29, 31, 33, 34, 35, 36,
37, 38, 39, 40, 41, 42, 43, 44,
46, 48, 49, 50, 51, 52, 53, 54,
55, 56, 57, 58, 59, 60, 61, 62,
64, 65, 66, 67, 68, 69, 70, 71,
72, 73, 74, 75, 76, 77, 78, 79,
81, 82, 83, 84, 85, 86, 87, 88,
89, 90, 91, 92, 93, 94, 95, 96,
97, 98, 99, 100,101,102,103,104,
105,106,107,108,109,110,111,112,
113,114,115,116,117,118,119,120,
121,122,123,124,125,126,127,128
};
unsigned char _a2u[128] = { /* A- to u-law conversions */
1, 3, 5, 7, 9, 11, 13, 15,
16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31,
32, 32, 33, 33, 34, 34, 35, 35,
36, 37, 38, 39, 40, 41, 42, 43,
44, 45, 46, 47, 48, 48, 49, 49,
50, 51, 52, 53, 54, 55, 56, 57,
58, 59, 60, 61, 62, 63, 64, 64,
65, 66, 67, 68, 69, 70, 71, 72,
73, 74, 75, 76, 77, 78, 79, 79,
80, 81, 82, 83, 84, 85, 86, 87,
88, 89, 90, 91, 92, 93, 94, 95,
96, 97, 98, 99, 100,101,102,103,
104,105,106,107,108,109,110,111,
112,113,114,115,116,117,118,119,
120,121,122,123,124,125,126,127
};
static int search(int val,short *table,int size)
{
int i;
for (i = 0; i < size; i++) {
if (val <= *table++)
return (i);
}
return (size);
}
/*********************************************************************
* 输入参数范围 :-32768~32767
* 返回8位无符号整数
* linear2alaw() - Convert a 16-bit linear PCM value to 8-bit A-law
*
* linear2alaw() accepts an 16-bit integer and encodes it as A-law data.
*
* Linear Input Code Compressed Code
* ----------------- ------------------
* 0000000wxyza 000wxyz
* 0000001wxyza 001wxyz
* 000001wxyzab 010wxyz
* 00001wxyzabc 011wxyz
* 0001wxyzabcd 100wxyz
* 001wxyzabcde 101wxyz
* 01wxyzabcdef 110wxyz
* 1wxyzabcdefg 111wxyz
*
* For further information see John C. Bellamy's Digital Telephony, 1982,
* John Wiley & Sons, pps 98-111 and 472-476.
*********************************************************************/
unsigned char linear2alaw(int pcm_val) /* 2's complement (16-bit range) */
{
int mask;
int seg;
unsigned char aval;
if (pcm_val >= 0) {
mask = 0xD5; /* sign (7th) bit = 1 */
} else {
mask = 0x55; /* sign bit = 0 */
//pcm_val = -pcm_val - 8;
pcm_val = -pcm_val - 1;
}
/* Convert the scaled magnitude to segment number. */
seg = search(pcm_val, seg_end, 8); //返回pcm_val属于哪个分段
/* Combine the sign, segment, and quantization bits. */
if (seg >= 8) /* out of range, return maximum value. */
return (0x7F ^ mask);
else {
aval = seg << SEG_SHIFT; //aval为每一段的偏移,分段量化后的数据需要加上该偏移(aval)
//分段量化
//量化方法: (pcm_val-分段值),然后取有效的高4位 (0分段例外)
//比如 pcm_val = 0x7000 ,那么seg=7 ,第7段的范围是0x4000~0x7FFF ,段偏移aval=7<<4=0x7F
//0x7000-0x4000=0x3000 ,然后取有效的高4位,即右移10(seg+3),0x3000>>10=0xC
//上一步等效为:(0x7000>>10)&0xF=0xC 。也就是: (pcm_val >> (seg + 3)) & QUANT_MASK
//然后加上段偏移 0x7F(aval) ,加法等效于或运算,即 |aval
if (seg < 2)
aval |= (pcm_val >> 4) & QUANT_MASK; //0、1段折线的斜率一样
else
aval |= (pcm_val >> (seg + 3)) & QUANT_MASK;
return (aval ^ mask); //异或0x55,目的是尽量避免出现连续的0,或连续的1,提高传输过程的可靠性
}
}
/*********************************************************************
* alaw2linear() - Convert an A-law value to 16-bit linear PCM
*********************************************************************/
int alaw2linear(unsigned char a_val)
{
int t;
int seg;
a_val ^= 0x55;
t = (a_val & QUANT_MASK) << 4;
seg = ((unsigned)a_val & SEG_MASK) >> SEG_SHIFT;
switch (seg) {
case 0:
t += 8;
break;
case 1:
t += 0x108;
break;
default:
t += 0x108;
t <<= seg - 1;
}
return ((a_val & SIGN_BIT) ? t : -t);
}
int main(int argc, char* argv[])
{
int cmp;
int dcmp;
int d;
while(1)
{
scanf("%d",&d); //输入16位的整数
printf("input:%d \n",d);
cmp=linear2alaw(d); //压缩成8位整数
dcmp=alaw2linear(cmp); //解压缩为16位整数
printf("cmp:%d , dcmp:%d \n",cmp,dcmp);
}
return 0;
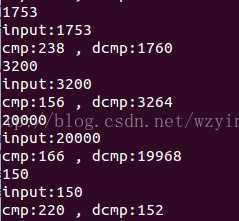
}运行结果:
对1753压缩后得到238,然后把238解压还原得到1760. 可以看出,还原后的数据,和原始数据还是相当接近的。输入
比较小的时候,还原误差小;输入大时,误差大。